Confounding Constructions

Lapo Tower is a new apartment building made of a proprietary material called 'Miracle MatterTM', and comprises of N layers, each of which has the same height but a different width.

Because of the interesting properties of 'Miracle MatterTM', each layer of Lapo Tower will only be stable if either it is resting on the ground, or its width is no greater than the average width of every layer beneath it. If a layer is unstable, it will crush the layer below it, destroying it completely. This will continue until the layer is stable (potentially crushing all the layers until it rests on the ground).

During construction, workers will place each layer sequentially on top of the next after waiting for the most recent layer to become stable. Your job is to determine how many layers Lapo Tower will have at the end of the construction process.

Input Format

The first line of input will contain a single integer N, representing the number of layers in Lapo Tower. The second line will contain N integers which represent the width of the layers, given in the order they will be placed.

Constraints

$0 \leq N \leq 100,000$. The width of any layer will be positive and at most 100,000.

Output Format

Your output should be a single integer, representing the number of layers in the final tower.

Sample Input 0

5
5 3 1 3 4

Sample Output 0

3

Explanation 0

1. The first layer to be placed is 5 units wide, and rests on the ground.
2. The next layer is 3 units wide, and since 3 is greater than the current average width (5 ÷ 1 = 5), this is stable on the 5-wide layer.
3. The third layer is 1 unit wide, and since the current average width is (5 + 3) ÷ 2 = 4, the layer is stable.
4. The fourth layer is 3 units wide, which is the same as the current average (5 + 3 + 1) ÷ 3 = 3, so the layer is stable.

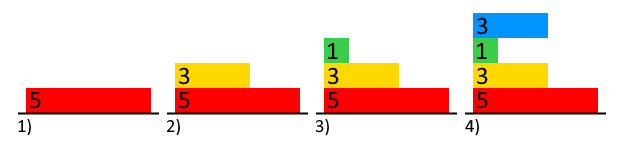
5. The final layer is 4 units wide, which is greater than the current average (5 + 3 + 1 + 3) ÷ 4 = 3, so it will destroy the top-most layer.
6. This brings the average width to (5 + 3 + 1) ÷ 3 = 3, which is still less than 4, so the top-most layer is destroyed again.
7. Now the average width of the remaining tower is (5 + 3) ÷ 2 = 4, which is equal to the width of the new layer, so the tower is stable. Therefore, the final tower has 3 layers, and your program should output 3.

Sample Input 1

4
10 20 30 30

Sample Output 1

2

Explanation 1

The 20 wide block will immediately crush the 10 block underneath, and will be crushed by the 30 wide block after it. The second 30 block can rest on the first, forming the final tower of [30, 30].